The Logical Playground of Socrates
Not too long ago I was introduced to a work that is supposedly a conversation that occurred between Socrates and a religious expert named Euthyphro. This is one of Plato’s early dialogues and was written shortly after the death of Socrates. I don’t intend on going into a great amount of detail in regards to the entire dialogue, so if you’d like to get the entire scope of the dialogue then I recommend you read it! I do think it would be a good idea to read it first before you read this blog post (although it won’t be necessary) to have complete clarity regarding the concepts I want to talk about. It is roughly 19 pages so it isn’t much of a burden to read; you can find a copy here.
The only real section of this dialogue I want to focus upon is when Socrates requests a definition of piety or holiness for the second time. By requesting a definition, Socrates is after the very essence of what it means to be holy. This turns out to be a very difficult thing for Euthyphro to attempt to define. Upon this second definition Socrates omits some unavoidable problems associated with the first definition. I do want to touch upon this for just a moment because it is rather important to point out that he altered this definition. The first definition was: “Holiness is what is loved by the Gods’.” Since their belief system was polytheistic, there were many different relationships and interactions that allowed for confusion to exist between the Gods’. This basically could be summed up by saying that what some Gods' hated some Gods' loved; thus such a definition could not represent an essence that could be applied to all objects to give them a universal attribute of being either holy or unholy based upon the Gods’ love. He points out that first a system must be consistent before any fundamental attributes can be ascribed to any elements within said system.
After this was pointed out they were at a bit of a stopping point, but Socrates was still curious and offered Euthyphro a solution out of this conundrum. Socrates suggests that they omit this issue and continue to try and find a definition for holiness. It was quite important for Socrates to explore this topic himself since he was being charged with corrupting the minds of the youth as well as being a supposed heretic. The solution he offered was to set all complications aside and make the issue black and white. He allowed for all the Gods’ then to be in union in regards to their love for all things and their hatred for all things. This essentially could also be viewed as unifying all Gods into one God that differentiates between holiness and unholiness. This is where the main point of the discussion comes into focus. Euthyphro’s new definition for holiness then becomes: “Holiness is what is loved by all the Gods’.” But to make this even more clear (for the more modern audience that is accustomed to a single God) I will modify the definition to: “Holiness is what is loved by God.”
Now to the core of the dialogue. I want to now express precisely what it was that Socrates did that I found to be incredibly insightful in order to demonstrate that the essence of holiness cannot be defined. We often think that we can create a simple binary system of actions that differentiate between holiness and unholiness, by say, placing them into some set A, and on the contrary all other unholy actions into set B. So let us pretend we are getting a sneak peek into some hypothetical God’s eyes and he is splitting all holy and unholy things into two sets: set A and B. This obviously appears to be an impossible thought experiment to conduct since Socrates already points out that there is a great deal of “grey area” or inconsistency in the world in regards to differentiating holy/unholy actions like this. Regardless, we have already omitted this issue and we are pretending we can see the world in black and white terms. So what is his plan now? In order to see through our hypothetical Godlike eyes we need to be able to know what holiness is to be able to decide how to appropriately place all the objects in the universe into their correct set.
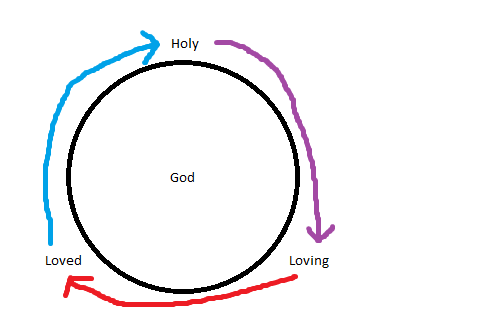
Now, the original definition Euthyphro gave us (Holiness is what is loved by God) can be looked at in two different ways. First we will start with: “things are holy because they are loved by God.” First, if someone loves some object X, then X is loved as a consequence of loving. We see here that a function of language arises in which verbs (actions) cause a consequence (upon something) which then leads to another word that describes a state produced by the action upon the subject. Socrates then provides a list of examples: To carry an apple results in it being carried, leading a person results in them being led, seeing an apple results in it being seen, and loving a person results in them being loved. We now know that in order to get to the word loved, there must first be an act of loving that produces the state of loved. So it appears that first God loves X, then X is loved, and finally X is holy by virtue of: “things are holy because they are loved by God.” So it appears that holiness is defined as that which is loved by God. How does holiness differ from being loved by God?
Socrates then asks: “Does God then love things because they are holy?” Why does he do this? We need to know how God loves to know why things then become holy once they are loved. Euthyphro wants to give Socrates a definition of holiness and he thinks he already has! We saw before that being loved, seen, or led are states that are brought about by loving, seeing, or leading. The definitions of the states that arise are dependent upon that which gives rise to it! So if being loved by God and holiness are synonymous then we should be able to say: “God loves things because they are loved by God.” If that seems confusing just think of it like this: being loved by God = holy and vice versa (by Euthyphro’s definition). A simple substitution demonstrates that this no longer makes sense! Being loved must be a consequence of loving, but in this case we see that Euthyphro is trying to claim that God’s loving is caused because he already loved things! How could that be? Something can’t be loved before the loving! This is a circular definition in which the word holy contains a faulty fundamental definition. We first have to know how God loves things before we can say anything about what something is by God’s love. In the previous paragraph we decided holiness was a quality of something produced by God’s loving. This shows that Socrates was in a way playing God by investigating whether it was possible for him to be able to tell whether something was holy or not prior to him deciding to love it! In the end no information can be provided that independently states what holiness is.
After thinking about this for a while I eventually was led to visualize a circle in which describes this problem fairly well (and leads me to my next point).
This revealed to me how important playful logical investigation is. Playing around with the order of things to determine how they interact and relate to one another has many applications. Many people after reading this believe that such discourse has the effect of being either positive or negative. The reason being in this particular example is that since Socrates demonstrated that Euthyphro had no true definition for holiness, he then could not act as a judge in regards to determining what actions he or others partook in would then be deemed holy or unholy in the eyes of the Gods’. This is pretty disorienting and upsetting to anyone who has been constructing their system of choices upon something that is then revealed to be without foundation. At some point in all of our lives we assume a certain degree of foundation in regards to reality in order to then give ourselves a starting point to base our next set of decisions. Many people consider that such a discussion is overall a negative one in regards to Socrates since he offers no other alternative for Euthyphro to base his decisions. Since Socrates focused on nothing other than seeking knowledge he effectively eliminated all possible explanations Euthyphro provided. By the same token, we can also say that this questioning by Socrates is also optimistic in that it eliminated information that was logically unsupportable and cleared the way for new solutions to potentially manifest. In a sense it is both a positive and negative discussion. What are people to do during the time in which there is no point of reference? How are people supposed to decide on what they should then do, and in what direction? Is it better to be free and wondering aimlessly until a new set of information arises to be analyzed or is it of more benefit to acknowledge the old system for what it can provide and cease with deconstruction due to flaws?
This is where I believe that it is best to view any system as a system that has no true objective foundation because it offers us the benefits of being able to play with it. We want to give it a foundation but at the same time we acknowledge that our starting point is only there precisely because we put it there and that’s all it should mean. We see that all of Euthyphro’s existence is defined by the system of piety that he clings to even though in the end it is shown to be incapable of explaining how pious actions should be categorized.
This leads me to a little summation in mathematics. Let’s say a teacher punished you (a student) by assigning you to add up all the numbers from 1 to 10. This seems to be a slightly annoying task in which you have to systematically add up each individual number like so: 1 + 2 + 3 + … + 10. So since this is boring you decide that you are going to investigate how numbers are added together a bit like Socrates investigated Euthyphro’s statement about holiness. We all are pretty familiar with the commutative property of mathematics in regards to addition. This is pretty important in establishing that our system is consistent regardless of how we choose to add up all our numbers from 1 – 10.
Now we could gather up all the number from one to 10 in many different ways. We are accustom to writing it as an ascending summation (1 + 2 + 3 … + 10). But we could write it as: 1 + 3 + 5 + 7 + 9 + 2 + 4 + 6 + 8 + 10. Or if we want to piss of the teacher–who may be checking our work–we could always scramble up all of our addition (1 + 7 + 3 + 9 + 4 + …). Could we make an argument for how we should do our summation? Is there a strong fundamental reason for adding things together in the traditional sense of summing up by increments of one? I suppose so, it is much easier to keep track of the number you are writing down and keeping things organized in a way in which we can much more easily visualize it.
Let’s say you just wanted to compare methods of ascending by one and descending by one.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 55
Well they both seem to be pretty much the same. What could be the utility of thinking about how you write down the summation? We already know that by the commutative law that it doesn’t matter how you add things together. Now Socrates would say that we have no concrete knowledge that should objectively direct us at how we should add these numbers together, but only that we know that they can be added together in any order really. So we have a belief that shows us the utility of adding our numbers together in ascending order by one because it is how we are taught to count and it is easy to visualize. But now that we’ve compared the two methods you have decided that you are so terribly bored with this exercise that you are going to play a game and add the two methods together. This is of course going to result in you adding up the numbers from one to ten twice but who cares?
(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) + (6 + 5) + (7 + 4) + (8 + 3) + (9 + 2) + (10 + 1) = 110
Which is of course 55 + 55 since you added them together.
But now we see a curious little pattern emerge from adding these two summations together.
(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) + (6 + 5) + (7 + 4) + (8 + 3) + (9 + 2) + (10 + 1)
=
11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11 + 11
=
(11)(10)
= 110.
Oh, and we had two groups of the same summation right?
(110)(1/2) = 55.
So what we were left with by adding these two groups together is a little formula. If we want to find out the sum of all the numbers from one to ten we can plug it into this formula:
n(n+1)/2
So it appears that by playing around with how we might decide to sum numbers together we’ve discovered a much more quick and efficient method to do so!